ARIMA

2017-05-04

Built using Zelig version 5.1.0.90000

Autoregressive and Moving-Average Models with Integration for Time-Series Data

Syntax

With reference classes:

z5 <- zarima$new()
z5$zelig(Y ~ X1 + X2, order = c(1,0,0), data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Y ~ X1 + X2, order = c(1,0,0), model = "arima", data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)

Additional Inputs

In addition, Zelig accepts the following additional inputs for arima to specify variables that provide the time index and any cross-sectional element if there are multiple time-series in the same dataset:

  • ts: Name of a variable that denotes the time element of the data. As a variable name, this should be in quotes. If this is not provided, Zelig will assume that the data is already ordered by time, but if provided, the dataset will be sorted by this variable before estimation.

  • cs: Name of a variable that denotes the cross-sectional element of the data, for example, country name in a dataset with time-series across different countries. As a variable name, this should be in quotes. If this is not provided, Zelig will assume that all observations come from the same unit over time, and should be pooled, but if provided, individual models will be run in each cross-section. If cs is given as an argument, ts must also be provided.

Examples

Single Series

Attach sample data, which has left party seat share and unemployment across time in several countries. We will subset to just those observations from the United Kingdom:

data(seatshare)
subset <- seatshare[seatshare$country == "UNITED KINGDOM",]

Estimate model:

ts.out <- zarima$new()
ts.out$zelig(unemp ~ leftseat, order = c(1,0,1), data = subset)

Summarize estimated model parameters:

summary(ts.out)
## Model: 
## 
## Call:
## ts.out$zelig(formula = unemp ~ leftseat, data = subset, order = c(1, 0, 1))
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.9028  0.8365     6.5782   -4.0245
## s.e.  0.0606  0.0986     1.9840    1.6622
## 
## sigma^2 estimated as 0.527:  log likelihood = -44.85,  aic = 99.71
## Next step: Use 'setx' method

Next we simulate what happens when leftseat share drops from a moderately high level of 75 percent, to a rather low level of 25 percent:

ts.out$setx(leftseat = 0.75)
ts.out$setx1(leftseat = 0.25)
ts.out$sim()
plot(ts.out)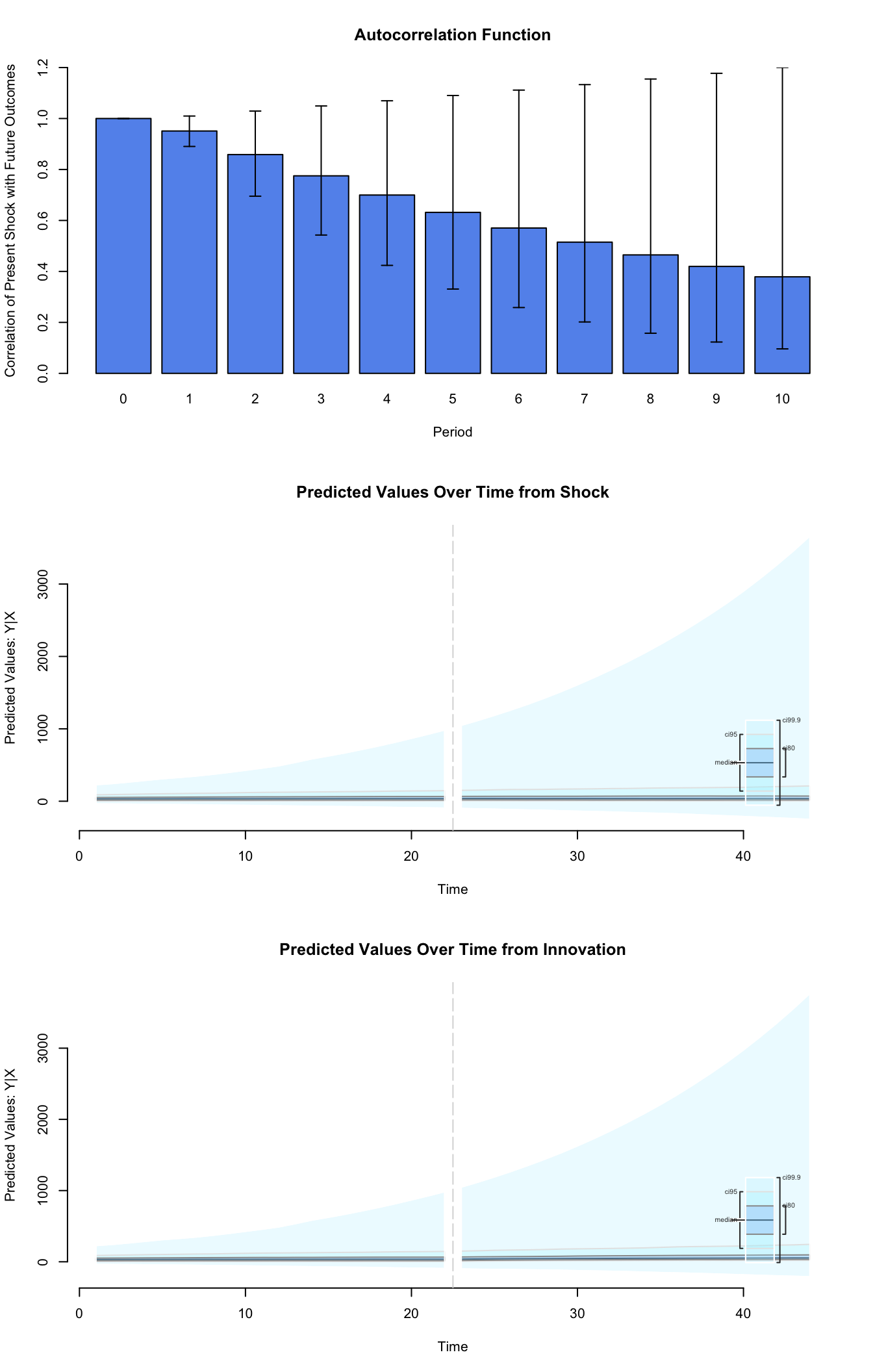
Graphs of Quantities of Interest for ARIMA models

Graphs of Quantities of Interest for ARIMA models

Multiple Series

The dataset contains similar series for 11 different OECD countries, and we could run the same model on each country’s data. Here we need to specify the ts and cs arguments to identify the names of variables that give the time and cross-section of each observation in the dataset

ts.out2 <- zarima$new()
ts.out2$zelig(unemp ~ leftseat, order = c(1,0,1), ts = "year",
              cs = "country", data = seatshare)
summary(ts.out2)
## Model: 
## $country
## [1] "AUSTRALIA"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.8849  0.5030     5.5878    0.5572
## s.e.  0.0807  0.1693     1.9419    2.0036
## 
## sigma^2 estimated as 0.8582:  log likelihood = -44.24,  aic = 98.47
## Model: 
## $country
## [1] "AUSTRIA"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.9553  0.7052     4.0325    1.5252
## s.e.  0.0395  0.1912     2.9062    5.3451
## 
## sigma^2 estimated as 0.1231:  log likelihood = -16.57,  aic = 43.14
## Model: 
## $country
## [1] "CANADA"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.8433  0.4100     7.7866   -0.3316
## s.e.  0.0819  0.1538     1.3222    1.4821
## 
## sigma^2 estimated as 0.7389:  log likelihood = -50.45,  aic = 110.89
## Model: 
## $country
## [1] "FINLAND"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##         ar1     ma1  intercept  leftseat
##       0.924  0.4631   -11.5415   21.2130
## s.e.  0.057  0.1089     8.8316   10.1507
## 
## sigma^2 estimated as 1.656:  log likelihood = -66.61,  aic = 143.23
## Model: 
## $country
## [1] "FRANCE"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.9850  0.4634     6.7010   -0.5321
## s.e.  0.0189  0.1666     4.1873    0.8049
## 
## sigma^2 estimated as 0.3057:  log likelihood = -31.18,  aic = 72.36
## Model: 
## $country
## [1] "ITALY"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.9613  0.5843    10.4435   -4.3455
## s.e.  0.0370  0.1384     2.5518    3.3636
## 
## sigma^2 estimated as 0.2537:  log likelihood = -30.54,  aic = 71.07
## Model: 
## $country
## [1] "NORWAY"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.8572  0.5438     5.4875   -5.3044
## s.e.  0.0890  0.1484     3.2045    6.3460
## 
## sigma^2 estimated as 0.2459:  log likelihood = -20.6,  aic = 51.19
## Model: 
## $country
## [1] "SPAIN"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.9496  0.9999    12.9842    0.7673
## s.e.  0.0537  0.1213     5.9394    3.7856
## 
## sigma^2 estimated as 1.179:  log likelihood = -36.4,  aic = 82.8
## Model: 
## $country
## [1] "SWEDEN"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.8303  1.0000     9.2331   -9.6728
## s.e.  0.0843  0.0849     1.4452    1.7366
## 
## sigma^2 estimated as 0.2909:  log likelihood = -32.65,  aic = 75.31
## Model: 
## $country
## [1] "UNITED KINGDOM"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.9028  0.8365     6.5782   -4.0245
## s.e.  0.0606  0.0986     1.9840    1.6622
## 
## sigma^2 estimated as 0.527:  log likelihood = -44.85,  aic = 99.71
## Model: 
## $country
## [1] "UNITED STATES"
## 
## 
## Call:
## ts.out2$zelig(formula = unemp ~ leftseat, data = seatshare, order = c(1, 0, 
##     1), ts = "year", cs = "country")
## 
## Coefficients:
##          ar1     ma1  intercept  leftseat
##       0.6518  0.3493     3.8765    3.6727
## s.e.  0.1586  0.2534     2.6929    4.4801
## 
## sigma^2 estimated as 0.7245:  log likelihood = -45.83,  aic = 101.66
## Next step: Use 'setx' method

See Also

The estimator used for ARIMA models is part of the stats package by William N. Venables and Brian D. Ripley .In addition, advanced users may wish to refer to help(arima).

R Core Team (2017). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. <URL: https://www.R-project.org/>.