Exponential Regression

Built using Zelig version 5.1.0.90000

Exponential Regression for Duration Dependent Variables with exp.

Use the exponential duration regression model if you have a dependent variable representing a duration (time until an event). The model assumes a constant hazard rate for all events. The dependent variable may be censored (for observations have not yet been completed when data were collected).

Syntax

With reference classes:

z5 <- zexp$new()
z5$zelig(Surv(Y, C) ~ X, weights = w, data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Surv(Y, C) ~ X, model = "exp", weights = w, data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)

Exponential models require that the dependent variable be in the form Surv(Y, C), where Y and C are vectors of length $n$. For each observation $i$ in 1, …, $n$, the value $y_i$ is the duration (lifetime, for example), and the associated $c_i$ is a binary variable such that $c_i = 1$ if the duration is not censored (e.g., the subject dies during the study) or $c_i = 0$ if the duration is censored (e.g., the subject is still alive at the end of the study and is know to live at least as long as $y_i$). If $c_i$ is omitted, all Y are assumed to be completed; that is, time defaults to 1 for all observations.

Input Values

In addition to the standard inputs, zelig() takes the following additional options for exponential regression:

robust: defaults to FALSE. If TRUE, zelig() computes robust standard errors based on sandwich estimators and the options selected in cluster.
cluster: if robust = TRUE, you may select a variable to define groups of correlated observations. Let x3 be a variable that consists of either discrete numeric values, character strings, or factors that define strata. Then

z.out <- zelig(y ~ x1 + x2, robust = TRUE, cluster = "x3",
               model = "exp", data = mydata)

means that the observations can be correlated within the strata defined by the variable x3, and that robust standard errors should be calculated according to those clusters. If robust = TRUE but cluster is not specified, zelig() assumes that each observation falls into its own cluster.

Example

Attach the sample data:

data(coalition)
library(survival)

Estimate the model:

z.out <- zelig(Surv(duration, ciep12) ~ fract + numst2, model = "exp",
               data = coalition)

View the regression output:

summary(z.out)

## Model: 
## 
## Call:
## z5$zelig(formula = Surv(duration, ciep12) ~ fract + numst2, data = coalition)
##                Value Std. Error     z        p
## (Intercept)  5.53587   0.547355 10.11 4.80e-24
## fract       -0.00391   0.000741 -5.27 1.35e-07
## numst2       0.46118   0.123895  3.72 1.97e-04
## 
## Scale fixed at 1 
## 
## Exponential distribution
## Loglik(model)= -1077.4   Loglik(intercept only)= -1100.7
##  Chisq= 46.66 on 2 degrees of freedom, p= 7.4e-11 
## Number of Newton-Raphson Iterations: 4 
## n= 314 
## 
## Next step: Use 'setx' method

Set the baseline values (with the ruling coalition in the minority) and the alternative values (with the ruling coalition in the majority) for X:

x.low <- setx(z.out, numst2 = 0)
x.high <- setx(z.out, numst2 = 1)

Simulate expected values and first differences:

s.out <- sim(z.out, x = x.low, x1 = x.high)

Summarize quantities of interest and produce some plots:

summary(s.out)

## 
##  sim x :
##  -----
## ev
##       mean      sd      50%     2.5%   97.5%
## 1 15.32519 1.49195 15.31858 12.63294 18.2208
## pv
##          mean       sd      50%      2.5%    97.5%
## [1,] 15.26937 15.06574 10.68142 0.3995287 57.02881
## 
##  sim x1 :
##  -----
## ev
##       mean       sd      50%     2.5%   97.5%
## 1 24.23103 1.868044 24.17358 20.77019 28.1369
## pv
##          mean       sd      50%      2.5%    97.5%
## [1,] 23.07127 23.15379 16.07259 0.5940207 84.32853
## fd
##       mean       sd      50%     2.5%    97.5%
## 1 8.905835 2.356881 8.876718 4.507367 13.74594

plot(s.out)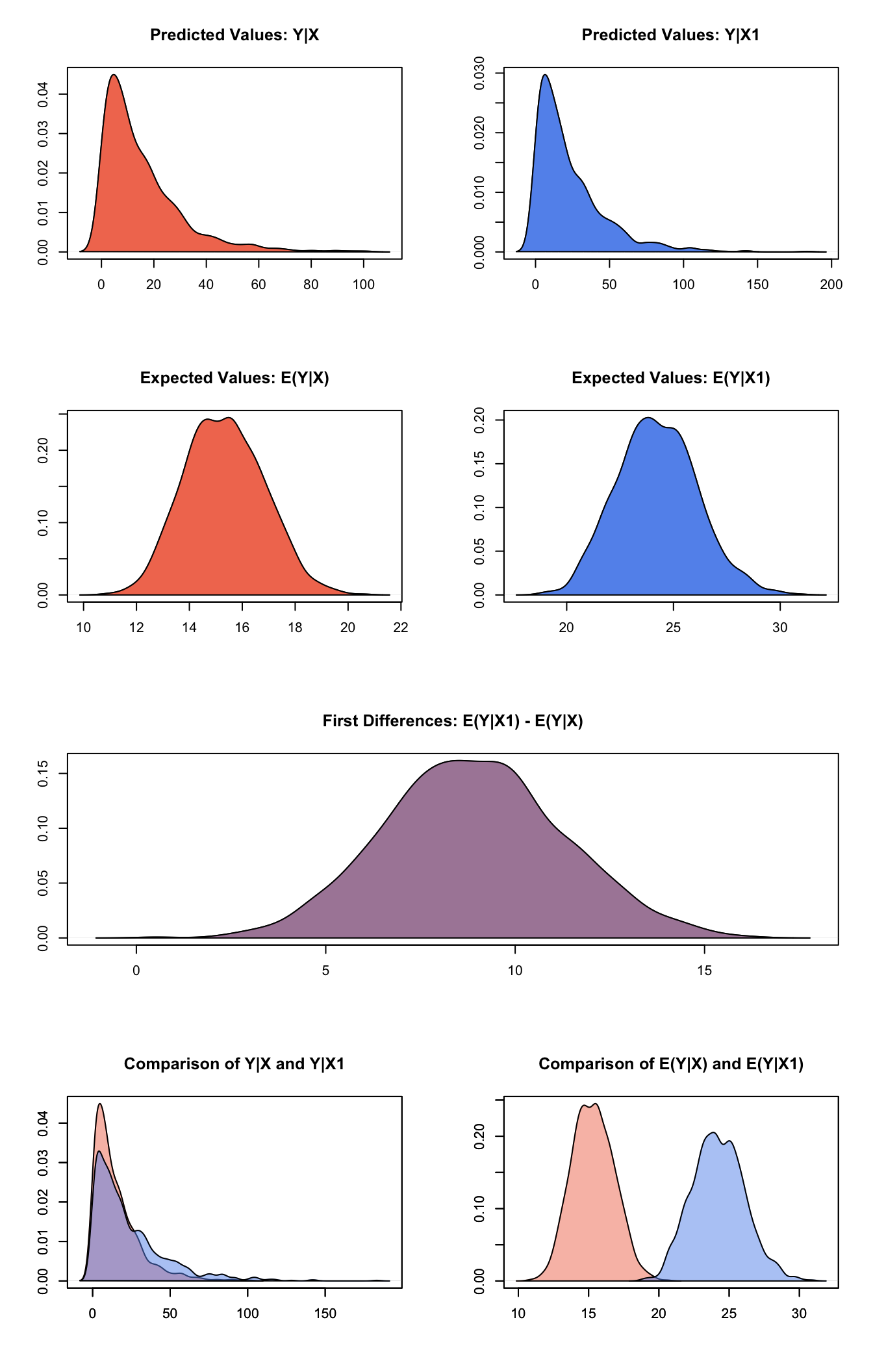

Graphs of Quantities of Interest for Zelig-exp

Model

Let $Y_i^*$ be the survival time for observation $i$. This variable might be censored for some observations at a fixed time $y_c$ such that the fully observed dependent variable, $Y_i$, is defined as

$$ Y_i = { \[\begin{array}{ll} Y_i^* & \textrm{if }Y_i^* \leq y_c \\ y_c & \textrm{if }Y_i^* > y_c \\ \end{array}\]

The stochastic component is described by the distribution of the partially observed variable $Y^*$. We assume $Y_i^*$ follows the exponential distribution whose density function is given by

\[ f(y_i^*\mid \lambda_i) = \frac{1}{\lambda_i} \exp\left(-\frac{y_i^*}{\lambda_i}\right) \]

for $y_i^*\ge 0$ and $\lambda_i>0$. The mean of this distribution is $\lambda_i$.

In addition, survival models like the exponential have three additional properties. The hazard function $h(t)$ measures the probability of not surviving past time $t$ given survival up to $t$. In general, the hazard function is equal to $f(t)/S(t)$ where the survival function $S(t) = 1 - \int_{0}^t f(s) ds$ represents the fraction still surviving at time $t$. The cumulative hazard function $H(t)$ describes the probability of dying before time $t$. In general, $H(t)= \int_{0}^{t} h(s) ds = -\log S(t)$. In the case of the exponential model,

$$ \[\begin{aligned} h(t) &=& \frac{1}{\lambda_i} \\ S(t) &=& \exp\left( -\frac{t}{\lambda_i} \right) \\ H(t) &=& \frac{t}{\lambda_i}\end{aligned}\]

For the exponential model, the hazard function $h(t)$ is constant over time. The Weibull model and lognormal models allow the hazard function to vary as a function of elapsed time (see and respectively).

The systematic component $\lambda_i$ is modeled as

\[ \lambda_i = \exp(x_i \beta), \]

where $x_i$ is the vector of explanatory variables, and $\beta$ is the vector of coefficients.

Quantities of Interest

The expected values (qi$ev) for the exponential model are simulations of the expected duration given $x_i$ and draws of $\beta$ from its posterior,

\[ E(Y) = \lambda_i^{-1} = 1/\exp(x_i \beta). \]

The predicted values (qi$pr) are draws from the exponential distribution with rate equal to the expected value.
The first difference (or difference in expected values, qi$ev.diff), is

\[ \textrm{FD} \; = \; E(Y \mid x_1) - E(Y \mid x), \]

where $x$ and $x_1$ are different vectors of values for the explanatory variables.

In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - E[Y_i(t_i=0)] \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. When $Y_i(t_i=1)$ is censored rather than observed, we replace it with a simulation from the model given available knowledge of the censoring process. Variation in the simulations is due to two factors: uncertainty in the imputation process for censored $y_i^*$ and uncertainty in simulating $E[Y_i(t_i=0)]$, the counterfactual expected value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - \widehat{Y_i(t_i=0)} \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. When $Y_i(t_i=1)$ is censored rather than observed, we replace it with a simulation from the model given available knowledge of the censoring process. Variation in the simulations is due to two factors: uncertainty in the imputation process for censored $y_i^*$ and uncertainty in simulating $\widehat{Y_i(t_i=0)}$, the counterfactual predicted value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

Output Values

The Zelig object stores fields containing everything needed to rerun the Zelig output, and all the results and simulations as they are generated. In addition to the summary commands demonstrated above, some simply utility functions (known as getters) provide easy access to the raw fields most commonly of use for further investigation.

In the example above z.out$get_coef() returns the estimated coefficients, z.out$get_vcov() returns the estimated covariance matrix, and z.out$get_predict() provides predicted values for all observations in the dataset from the analysis.

2017-05-04