Gamma Regression

Built using Zelig version 5.1.0.90000

Gamma Regression for Continuous, Positive Dependent Variables with gamma.

Use the gamma regression model if you have a positive-valued dependent variable such as the number of years a parliamentary cabinet endures, or the seconds you can stay airborne while jumping. The gamma distribution assumes that all waiting times are complete by the end of the study (censoring is not allowed).

Syntax

With reference classes:

z5 <- zgamma$new()
z5$zelig(Y ~ X1 + X ~ X, weights = w, data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Y ~ X1 + X2, model = "gamma", weights = w, data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out, x1 = NULL)

Example

Attach the sample data:

data(coalition)

Estimate the model:

z.out <- zelig(duration ~ fract + numst2, model = "gamma", data = coalition)

View the regression output:

summary(z.out)

## Model: 
## 
## Call:
## z5$zelig(formula = duration ~ fract + numst2, data = coalition)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.2510  -0.9112  -0.2278   0.4132   1.5360  
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.296e-02  1.329e-02  -0.975  0.33016
## fract        1.149e-04  1.723e-05   6.668 1.19e-10
## numst2      -1.739e-02  5.881e-03  -2.957  0.00335
## 
## (Dispersion parameter for Gamma family taken to be 0.6291004)
## 
##     Null deviance: 300.74  on 313  degrees of freedom
## Residual deviance: 272.19  on 311  degrees of freedom
## AIC: 2428.1
## 
## Number of Fisher Scoring iterations: 6
## 
## Next step: Use 'setx' method

Set the baseline values (with the ruling coalition in the minority) and the alternative values (with the ruling coalition in the majority) for X:

x.low <- setx(z.out, numst2 = 0)
x.high <- setx(z.out, numst2 = 1)

Simulate expected values (qi$ev) and first differences (qi$fd):

s.out <- sim(z.out, x = x.low, x1 = x.high)

summary(s.out)

## 
##  sim x :
##  -----
## ev
##         mean       sd      50%     2.5%   97.5%
## [1,] 14.4043 1.061457 14.33427 12.47827 16.6991
## pv
##          mean       sd      50%      2.5%   97.5%
## [1,] 13.86111 12.33949 10.67768 0.5294782 44.9441
## 
##  sim x1 :
##  -----
## ev
##         mean       sd      50%    2.5%    97.5%
## [1,] 19.2101 1.090567 19.13691 17.2235 21.56033
## pv
##          mean       sd      50%     2.5%    97.5%
## [1,] 19.86033 18.47412 14.55303 1.020767 65.90548
## fd
##          mean       sd      50%     2.5%    97.5%
## [1,] 4.805793 1.499152 4.820032 1.881295 7.811935

plot(s.out)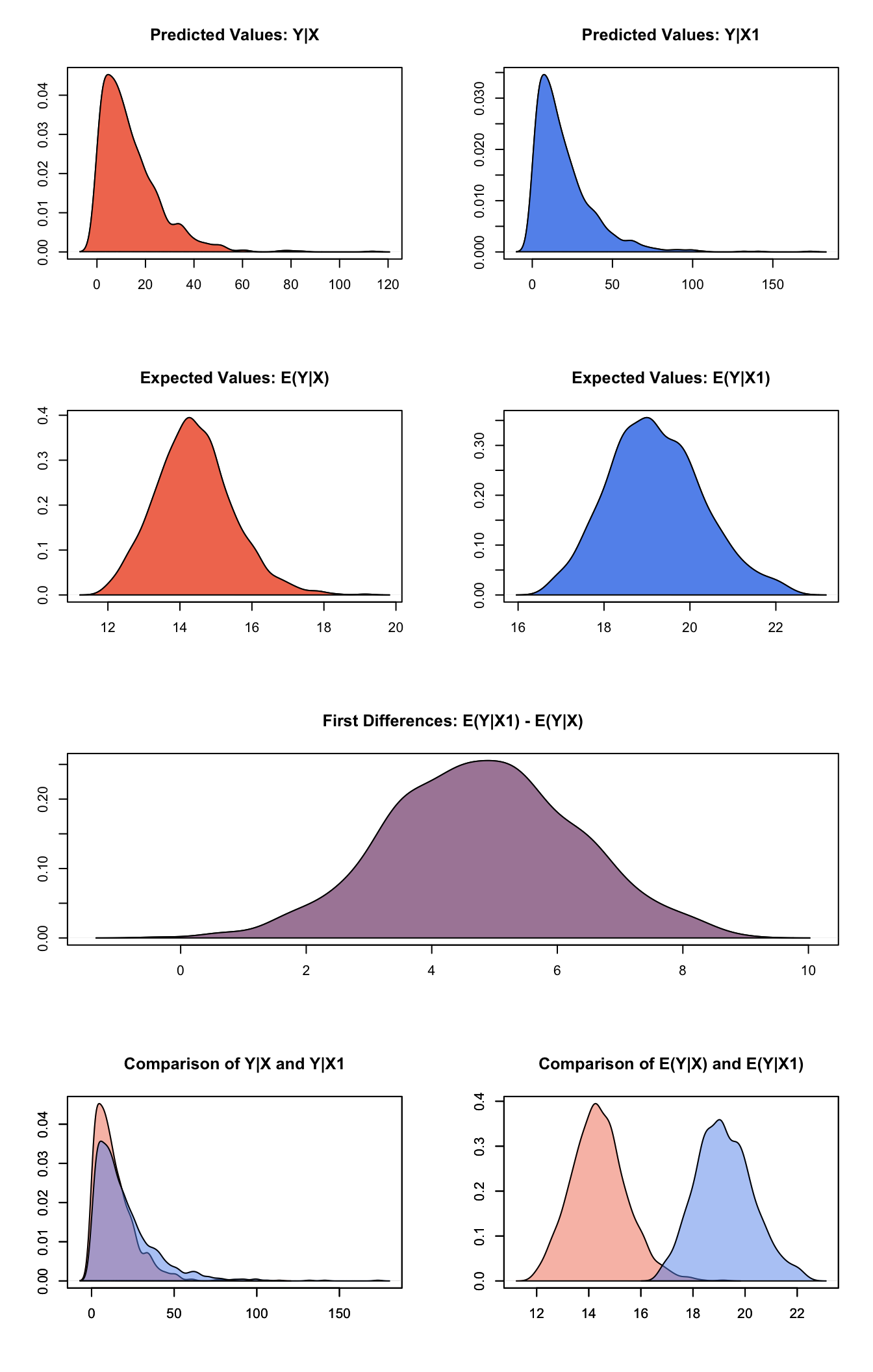

Graphs of Quantities of Interest for Zelig-gamma

Model

The Gamma distribution with scale parameter $\alpha$ has a stochastic component:

$$ \[\begin{aligned} Y &\sim& \textrm{Gamma}(y_i \mid \lambda_i, \alpha) \\ f(y) &=& \frac{1}{\alpha^{\lambda_i} \, \Gamma \lambda_i} \, y_i^{\lambda_i - 1} \exp -\left\{ \frac{y_i}{\alpha} \right\}\end{aligned}\]

for $\alpha, \lambda_i, y_i > 0$.

The systematic component is given by

\[ \lambda_i = \frac{1}{x_i \beta} \]

Quantities of Interest

The expected values (qi$ev) are simulations of the mean of the stochastic component given draws of $\alpha$ and $\beta$ from their posteriors:

\[ E(Y) = \alpha \lambda_i. \]

The predicted values (qi$pr) are draws from the gamma distribution for each given set of parameters $(\alpha, \lambda_i)$.
If x1 is specified, sim() also returns the differences in the expected values (qi$fd),

\[ E(Y \mid x_1) - E(Y \mid x) \]

In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - E[Y_i(t_i=0)] \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $E[Y_i(t_i=0)]$, the counterfactual expected value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - \widehat{Y_i(t_i=0)} \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $\widehat{Y_i(t_i=0)}$, the counterfactual predicted value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

Output Values

The Zelig object stores fields containing everything needed to rerun the Zelig output, and all the results and simulations as they are generated. In addition to the summary commands demonstrated above, some simply utility functions (known as getters) provide easy access to the raw fields most commonly of use for further investigation.

In the example above z.out$get_coef() returns the estimated coefficients, z.out$get_vcov() returns the estimated covariance matrix, and z.out$get_predict() provides predicted values for all observations in the dataset from the analysis.

2017-05-04

Syntax

Example

Model

Quantities of Interest

Output Values

See also

Contents