Normal Survey Regression

Built using Zelig version 5.1.0.90000

Normal Regression for Continuous Dependent Variables with Survey Weights with normal.survey.

The Normal regression model is a close variant of the more standard least squares regression model (see ). Both models specify a continuous dependent variable as a linear function of a set of explanatory variables. The Normal model reports maximum likelihood (rather than least squares) estimates. The two models differ only in their estimate for the stochastic parameter $\sigma$.

Syntax

With reference classes:

z5 <- znormalsurvey$new()
z5$zelig(Y ~ X1 + X ~ X, weights = w, data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Y ~ X1 + X2, model = "normal.survey", weights = w,
               data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)

Examples

Example 1: User has Existing Sample Weights

Attach sample data and variable names:

data(api, package = "survey")

In this example, we will estimate a model using the percentages of students who receive subsidized lunch and an indicator for whether schooling is year-round to predict California public schools’ academic performance index scores:

z.out1 <- zelig(api00 ~ meals + yr.rnd, model = "normal.survey",
                weights=~pw, data = apistrat)

## Warning: Supplied weights argument is not a vector or a variable name in the dataset, and will be ignored.

summary(z.out1)

## Model: 
## 
## Call:
## z5$zelig(formula = api00 ~ meals + yr.rnd, data = apistrat, weights = ~pw)
## 
## Survey design:
## survey::svydesign(data = data, ids = ids, probs = probs, strata = strata, 
##     fpc = fpc, nest = nest, check.strata = check.strata, weights = localWeights)
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) 825.1058     9.3912  87.859   <2e-16
## meals        -3.3581     0.1698 -19.781   <2e-16
## yr.rndYes    -6.3855    15.4044  -0.415    0.679
## 
## (Dispersion parameter for gaussian family taken to be 5225.087)
## 
## Number of Fisher Scoring iterations: 2
## 
## Next step: Use 'setx' method

Set explanatory variables to their default (mean/mode) values, and set a high (80th percentile) and low (20th percentile) value for “meals,” the percentage of students who receive subsidized meals:

x.low <- setx(z.out1, meals= quantile(apistrat$meals, 0.2))
x.high <- setx(z.out1, meals= quantile(apistrat$meals, 0.8))

Generate first differences for the effect of high versus low “meals” on academic performance:

s.out1 <- sim(z.out1, x = x.high, x1 = x.low)
summary(s.out1)

## 
##  sim x :
##  -----
## ev
##          mean       sd      50%     2.5%    97.5%
## [1,] 576.0741 7.212141 576.0612 561.5907 590.8942
## pv
##          mean       sd      50%    2.5%    97.5%
## [1,] 579.6753 69.44799 580.0193 444.056 712.7222
## 
##  sim x1 :
##  -----
## ev
##          mean      sd      50%     2.5%    97.5%
## [1,] 764.4627 7.03601 764.5055 750.5694 778.5018
## pv
##          mean       sd      50%     2.5%    97.5%
## [1,] 765.1266 72.34414 762.6121 628.5771 909.8353
## fd
##          mean       sd      50%     2.5%    97.5%
## [1,] 188.3887 9.346978 188.5047 170.1059 206.7381

Generate a second set of fitted values and a plot:

plot(s.out1)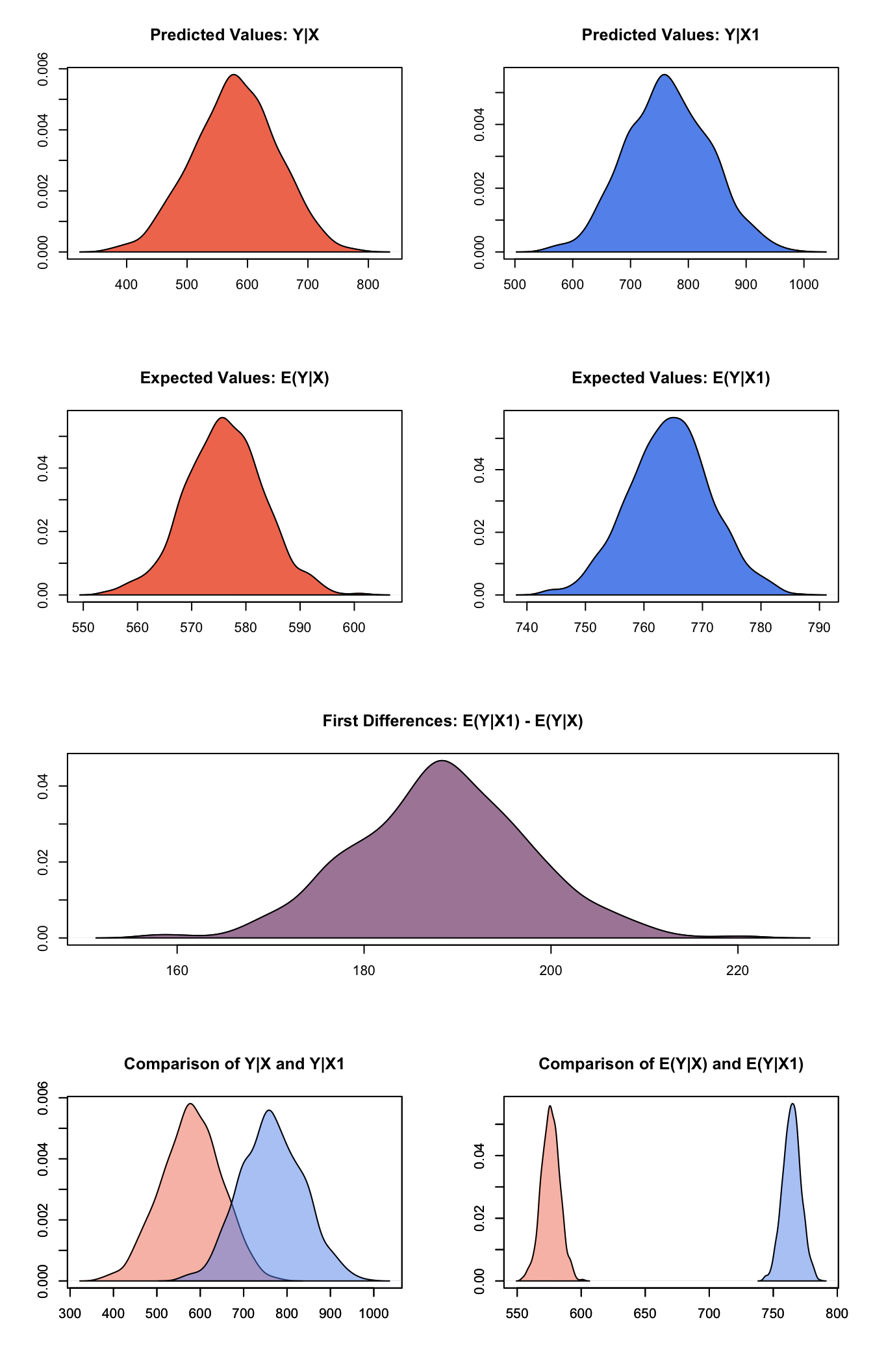

Graphs of Quantities of Interest for Normal Survey Model

Example 2: User has Details about Complex Survey Design (but not sample weights)

Suppose that the survey house that provided the dataset excluded probability weights but made other details about the survey design available. We can still estimate a model without probability weights that takes instead variables that identify each the stratum and/or cluster from which each observation was selected and the size of the finite sample from which each observation was selected.

z.out2 <- zelig(api00 ~ meals + yr.rnd, model = "normal.survey",
                strata = ~stype, fpc = ~fpc, data = apistrat)
summary(z.out2)

## Model: 
## 
## Call:
## z5$zelig(formula = api00 ~ meals + yr.rnd, data = apistrat, strata = ~stype, 
##     fpc = ~fpc)
## 
## Survey design:
## survey::svydesign(data = data, ids = ids, probs = probs, strata = strata, 
##     fpc = fpc, nest = nest, check.strata = check.strata, weights = localWeights)
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) 825.1058     8.3552  98.753   <2e-16
## meals        -3.3581     0.1644 -20.430   <2e-16
## yr.rndYes    -6.3855    15.1624  -0.421    0.674
## 
## (Dispersion parameter for gaussian family taken to be 5225.087)
## 
## Number of Fisher Scoring iterations: 2
## 
## Next step: Use 'setx' method

Note that these results are identical to the results obtained when pre-existing sampling weights were used. When sampling weights are omitted, Zelig estimates them automatically for “normal.survey” models based on the user-defined description of sampling designs. If no description is present, the default assumption is equal probability sampling.

The methods setx() and sim() can then be run on z.out2 in the same fashion described in Example 1.

Example 3: User has Replicate Weights

Load data for a model using the number of out-of-hospital cardiac arrests to predict the number of patients who arrive alive in hospitals:

data(scd, package = "survey")

Create four Balanced Repeated Replicate (BRR) weights:

BRRrep <- 2*cbind(c(1,0,1,0,1,0), c(1,0,0,1,0,1),
                c(0,1,1,0,0,1), c(0,1,0,1,1,0))

Estimate the model using Zelig:

z.out3 <- zelig(formula=alive ~ arrests , model = "normal.survey",
                repweights = BRRrep, type = "BRR",
                data = scd, na.action = NULL)

## Warning in svrepdesign.default(data = data, repweights = repweights, type =
## type, : No sampling weights provided: equal probability assumed

summary(z.out3)

## Model: 
## 
## Call:
## z5$zelig(formula = alive ~ arrests, data = scd, repweights = BRRrep, 
##     type = "BRR", na.action = NULL)
## 
## Survey design:
## svrepdesign.default(data = data, repweights = repweights, type = type, 
##     weights = localWeights, combined.weights = combined.weights, 
##     rho = rho, bootstrap.average = bootstrap.average, scale = scale, 
##     rscales = rscales, fpctype = fpctype, fpc = fpc)
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept) 16.777828   3.949296   4.248  0.05119
## arrests      0.097920   0.006064  16.149  0.00381
## 
## (Dispersion parameter for gaussian family taken to be 23.65681)
## 
## Number of Fisher Scoring iterations: 2
## 
## Next step: Use 'setx' method

Set the explanatory variable at its minimum and maximum

x.min <- setx(z.out3, arrests = min(scd$alive))
x.max <- setx(z.out3, arrests = max(scd$alive))

Generate first differences for the effect of the minimum versus the maximum number of cardiac arrests on the number of people who arrive alive:

s.out3 <- sim(z.out3, x=x.max, x1=x.min)
summary(s.out3)

## 
##  sim x :
##  -----
## ev
##          mean       sd      50%     2.5%    97.5%
## [1,] 24.47312 3.603297 24.56658 17.75726 31.51732
## pv
##          mean       sd      50%    2.5%    97.5%
## [1,] 24.41233 12.22076 24.53819 2.84381 45.37047
## 
##  sim x1 :
##  -----
## ev
##          mean       sd      50%     2.5%    97.5%
## [1,] 18.97948 3.876408 19.06842 11.69499 26.37252
## pv
##          mean      sd      50%       2.5%   97.5%
## [1,] 19.47485 12.3683 18.89057 -0.7115458 40.6895
## fd
##           mean        sd       50%      2.5%    97.5%
## [1,] -5.493631 0.3337031 -5.489195 -6.142893 -4.83746

Generate a second set of fitted values and a plot:

plot(s.out3)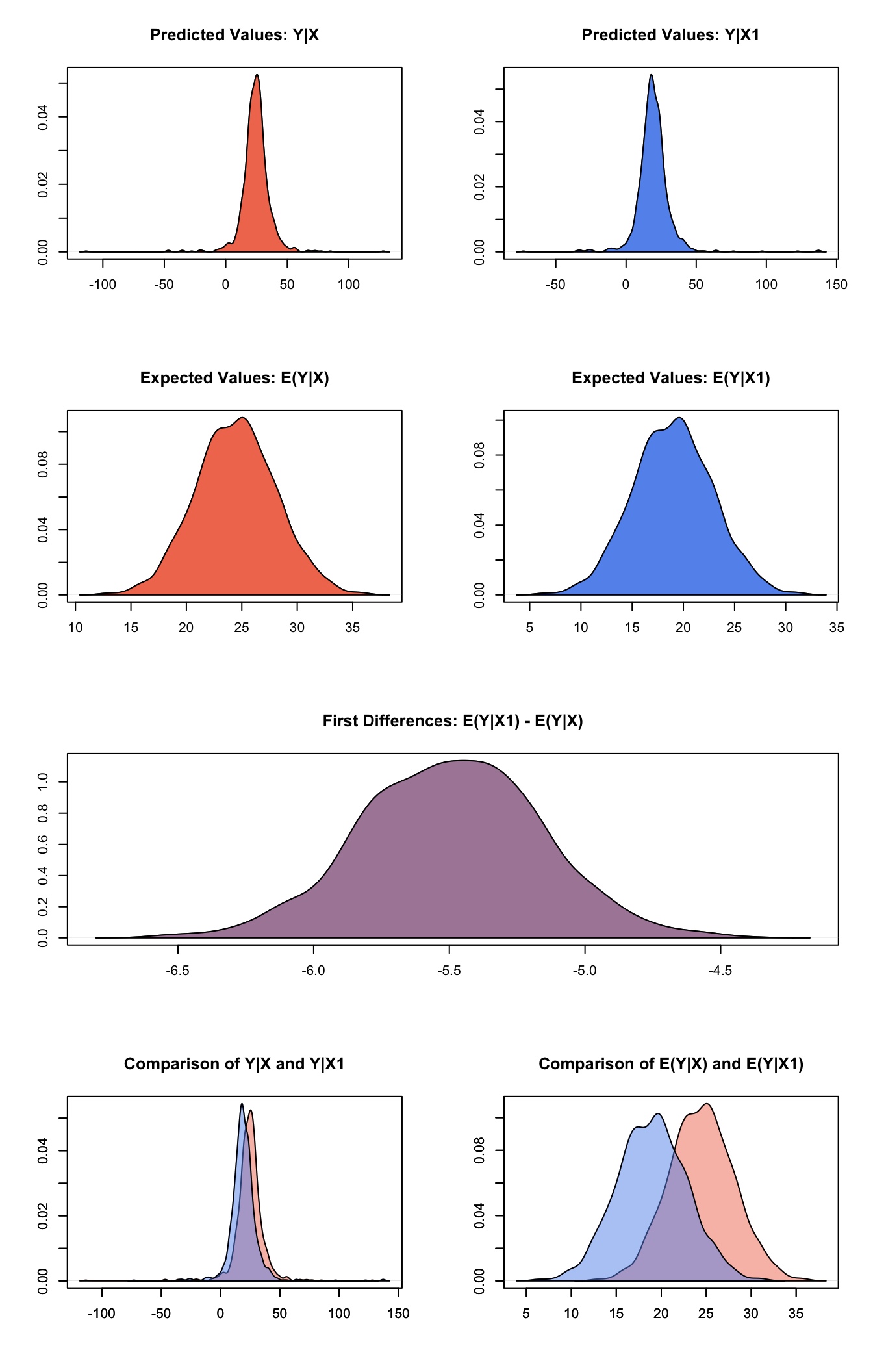

Graphs of Quantities of Interest for Normal Survey Model

The user should also refer to the normal model demo, since normal.survey models can take many of the same options as normal models.

Model

Let $Y_i$ be the continuous dependent variable for observation $i$.

The stochastic component is described by a univariate normal model with a vector of means $\mu_i$ and scalar variance $\sigma^2$:

\[ Y_i \; \sim \; \textrm{Normal}(\mu_i, \sigma^2). \]

The systematic component is

\[ \mu_i \;= \; x_i \beta, \]

where $x_i$ is the vector of $k$ explanatory variables and $\beta$ is the vector of coefficients.

Quantities of Interest

The expected value (qi$ev) is the mean of simulations from the the stochastic component,

\[ E(Y) = \mu_i = x_i \beta, \]

given a draw of $\beta$ from its posterior.

The predicted value (qi$pr) is drawn from the distribution defined by the set of parameters $(\mu_i, \sigma)$.
The first difference (qi$fd) is:

\[ \textrm{FD}\; = \;E(Y \mid x_1) - E(Y \mid x) \]

In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - E[Y_i(t_i=0)] \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $E[Y_i(t_i=0)]$, the counterfactual expected value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - \widehat{Y_i(t_i=0)} \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $\widehat{Y_i(t_i=0)}$, the counterfactual predicted value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

Output Values

The Zelig object stores fields containing everything needed to rerun the Zelig output, and all the results and simulations as they are generated. In addition to the summary commands demonstrated above, some simply utility functions (known as getters) provide easy access to the raw fields most commonly of use for further investigation.

In the example above z.out$get_coef() returns the estimated coefficients, z.out$get_vcov() returns the estimated covariance matrix, and z.out$get_predict() provides predicted values for all observations in the dataset from the analysis.

2017-05-04