Probit Regression

Built using Zelig version 5.1.0.90000

Probit Regression for Dichotomous Dependent Variables with probit.

Use probit regression to model binary dependent variables specified as a function of a set of explanatory variables.

Syntax

With reference classes:

z5 <- zprobit$new()
z5$zelig(Y ~ X1 + X ~ X, weights = w, data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Y ~ X1 + X2, model = "probit", weights = w,
               data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out, x1 = NULL)

Example

Attach the sample turnout dataset:

data(turnout)

Estimate parameter values for the probit regression:

z.out <- zelig(vote ~ race + educate, model = "probit", data = turnout)

summary(z.out)

## Model: 
## 
## Call:
## z5$zelig(formula = vote ~ race + educate, data = turnout)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.2586  -0.8982   0.6712   0.7232   1.7045  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.725949   0.128635  -5.643 1.67e-08
## racewhite    0.299076   0.084648   3.533 0.000411
## educate      0.097119   0.009571  10.147  < 2e-16
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 2266.7  on 1999  degrees of freedom
## Residual deviance: 2136.0  on 1997  degrees of freedom
## AIC: 2142
## 
## Number of Fisher Scoring iterations: 4
## 
## Next step: Use 'setx' method

Set values for the explanatory variables to their default values.

x.out <- setx(z.out)

Simulate quantities of interest from the posterior distribution.

s.out <- sim(z.out, x = x.out)

summary(s.out)

plot(s.out)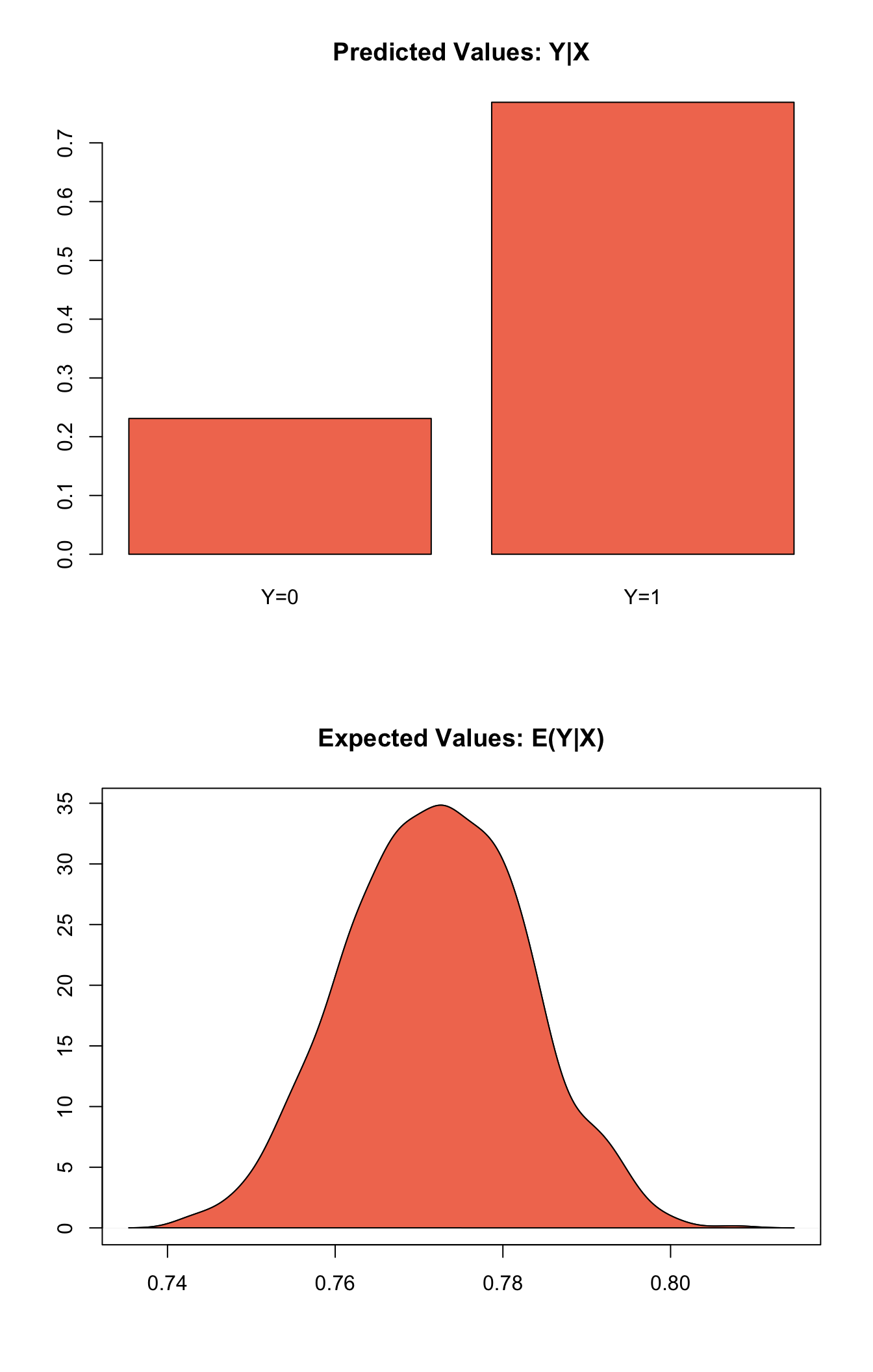

Graphs of Quantities of Interest for Zelig-probit

Model

Let $Y_i$ be the observed binary dependent variable for observation $i$ which takes the value of either 0 or 1.

The stochastic component is given by

\[ Y_i \; \sim \; \textrm{Bernoulli}(\pi_i), \]

where $\pi_i=\Pr(Y_i=1)$.

The systematic component is

\[ \pi_i \; = \; \Phi (x_i \beta) \]

where $\Phi(\mu)$ is the cumulative distribution function of the Normal distribution with mean 0 and unit variance.

Quantities of Interest

The expected value (qi$ev) is a simulation of predicted probability of success

\[ E(Y) = \pi_i = \Phi(x_i \beta), \]

given a draw of $\beta$ from its sampling distribution.

The predicted value (qi$pr) is a draw from a Bernoulli distribution with mean $\pi_i$.
The first difference (qi$fd) in expected values is defined as

\[ \textrm{FD} = \Pr(Y = 1 \mid x_1) - \Pr(Y = 1 \mid x). \]

The risk ratio (qi$rr) is defined as

\[ \textrm{RR} = \Pr(Y = 1 \mid x_1) / \Pr(Y = 1 \mid x). \]

In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - E[Y_i(t_i=0)] \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $E[Y_i(t_i=0)]$, the counterfactual expected value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - \widehat{Y_i(t_i=0)} \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $\widehat{Y_i(t_i=0)}$, the counterfactual predicted value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

Output Values

The Zelig object stores fields containing everything needed to rerun the Zelig output, and all the results and simulations as they are generated. In addition to the summary commands demonstrated above, some simply utility functions (known as getters) provide easy access to the raw fields most commonly of use for further investigation.

In the example above z.out$get_coef() returns the estimated coefficients, z.out$get_vcov() returns the estimated covariance matrix, and z.out$get_predict() provides predicted values for all observations in the dataset from the analysis.

2017-05-04

Syntax

Example

Model

Quantities of Interest

Output Values

See also

Contents